Comportamiento choca-gira: retoque final

Detecté pero no arreglé un pequeño problema derivado de calcular si ha llegado el robot o no al ángulo de destino. Ahora toca arreglar ese defecto para que la práctica sea completa.

Para comprender el problema debemos saber dos cosas del robot:

Los sensores de orientación del robot no son perfectos, por consiguiente la brújula tiene un margen de error y una granularidad que impide la búsqueda de un ángulo de destino perfecto. Por consiguiente no se busca un ángulo de destino, si no un ángulo de destino con un margen de error de varios grados.

En la imagen puede verse una representación del ángulo de destino:

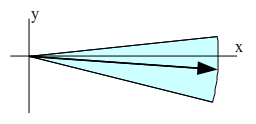
En ella puede verse el ángulo de destino (356º) y el margen de error anterior (356º - 10º = 346º) y posterior (356º + 10º = 366º = 6º).

¿Qué problema existe en la búsqueda de ese sentido de orientación?

Para averiguar si ha llegado o no el robot a su orientación de destino restamos los ángulos destino y actual y obtenemos el valor absoluto.

φ = | φ_r - φ_f |

Donde φ_r es la orientación actual del robot y φ_d la orientación final a la que debe llegar.

Veamos varios ejemplos de cómo se comporta este mecanismo de cálculo con varios ejemplos:

• Estamos en 340º: |340 - 356| = 16 (> 10 fuera del margen - CORRECTO).
• Estamos en 349º: |349 - 356| = 7 (< 10 dentro del marge - CORRECTO).
• Estamos en 358º: |340 - 356| = 2 (< 10 dentro del margen - CORRECTO).
• Estamos en 4º: |4 - 356| = 352 (> 10 fuera del margen - INCORRECTO).
• Estamos en 8º: |8 - 356| = 348 (> 10 fuera del margen - CORRECTO).

Podemos resumir el comportamiento de este cálculo en la siguiente ilustración:

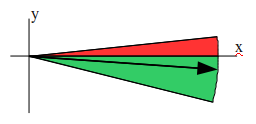
En ella podemos ver que cuando el ángulo es cercano al destino pero éste no "cruza" el eje de abscisas todo funciona correctamente (zona verde) pero si estamos dentro de un ángulo al otro lado del eje de abscisas entonces nos encontramos con que los cálculos fallan.

¿Cómo arreglarlo?

Existen varias soluciones. La que proponen en clase es comprobar cuándo el robot puede verse involucrado en este tipo de situaciones y modificar el cálculo de la diferencia en ese caso.

¿Cómo?

Veamos la siguiente ilustración:

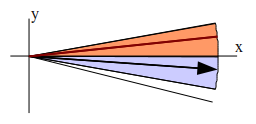
Podemos ver dos zonas la anaranjada y la azulada. Corresponden al arco comprendido entre 10º y 0º (zona anaranjada) y de 0º a -10º (zona azulada).

Podríamos hacer sectores y comprobar cuándo pasan por el eje de abscisas y arreglarlo. Una serie de sentencias condicionales nos ayudarían en la tarea.

Pero hay una forma más sencilla, comprobando únicamente cuándo el cálculo podría darnos problemas.

¿Cómo podríamos averiguar eso?

Podríamos hacer las siguientes comprobaciones:

• Si el robot está orientado en un ángulo inferior a 10º (zona anaranjada) y el destino es superior a 350º (zona azulada) le quitamos 360 grados al ángulo de destino.
• Si el robot está orientado en un ángulo superior a 350º (zona azulada) y el destino es inferior a 10º (zona anaranjada) le quitamos 360 grados al ángulo del robot.

Con eso los cálculos saldrían correctos. Podemos comprobarlo con los ejemplos anteriores.

Pensemos que la condición "el destino es superior a 350º" siempre se está cumpliendo de modo que sólo hay que restarle 360º al destino cuando el robot tiene su ángulo de giro por debajo de los 10º de margen:

• Estamos en 340º: |340 - 356| = 16 (> 10 fuera del margen - CORRECTO).
• Estamos en 349º: |349 - 356| = 7 (< 10 dentro del marge - CORRECTO).
• Estamos en 358º: |340 - 356| = 2 (< 10 dentro del margen - CORRECTO).
• Estamos en 4º: |4 - (356 - 360)| = |4 + 4)| = 8 (< 10 dentro del margen - CORRECTO).
• Estamos en 8º: |8 - (356 - 360)| = |8 + 4| = 12 (> 10 fuera del margen - CORRECTO).

¿Y no existe una solución más simple?

Casi siempre hay una solución mejor a la que inicialmente pensamos de forma natural.

Basta con restarle a 360º el ángulo calculado si éste supera los 180º.

Lo comprobamos con el ejemplo anterior:

• Estamos en 340º: |340 - 356| = 16 (> 10 fuera del margen - CORRECTO).
• Estamos en 349º: |349 - 356| = 7 (< 10 dentro del marge - CORRECTO).
• Estamos en 358º: |340 - 356| = 2 (< 10 dentro del margen - CORRECTO).
• Estamos en 4º: |4 - 356| = 352 -> 360 - 352 = 8 (< 10 dentro del margen - CORRECTO).
• Estamos en 8º: |8 - 356| = 348(*) -> 360 - 348 = 12 (> 10 fuera del margen - CORRECTO).

(*)Para minimizar el hitrate de dicha comprobación y ahorrarnos restas innecesarias comprobamos que únicamente esté por encima del margen superior, 350º, que será cuando nos interfiera en el cálculo en vez de hacerlo cada vez que supere los 180º.

En estos ejemplos hemos usado un error de 10º y hemos usado grados para facilitar los cálculos pero en la práctica el margen de error con el ángulo de destino es de tan sólo 5º y todos los cálculos se hacen en radianes.

En el siguiente vídeo muestro el funcionamiento del cálculo. Estamos calculando el ángulo de diferencia de manera continua, pero cuando la diferencia es mayor de 330º (360º - 30º) habilitamos el cálculo de corrección.

Hay que notar que en la práctica existen dos umbrales de decisión: <30º para girar más despacio y <5º para decidir que se ha llegado al objetivo. De modo que hay que tener en cuenta el umbral más bajo (360º - 30º) o no aplicar la optimización. De no hacerlo el robot podría pasar girando sobre los 5º de margen y pasarse en el giro, teniendo que completar una nueva vuelta y rezar que no vuelva a ocurrir lo mismo.