Usando una fuente de vídeo con OpenCV

Para usar una fuente de vídeo (webcam, cámara DV, capturadora, etc) deberemos hacer uso de las funciones cvCaptureFromCAM (inicialización del dispositivo de captura), cvQueryFrame (obtención de un fotograma) y cvReleaseCapture (liberar el dispositivo de captura).

Para mostrar la imagen de la webcam por pantalla haremos uso de las funciones cvNamedWindow (crear una ventana), cvShowImage (mostrar una imagen en una ventana previamente creada) y cvDestroyWindow (cerrar una ventana).

Por último, usaremos cvWaitKey para obtener la pulsación de una tecla antes del transcurso de un tiempo determinado para determinar el deseo del usuario de finalizar el programa capturando la pulsación de la tecla ESC.

El código es el siguiente:

Introducción al objetivo del proyecto

Una vez fijados los objetivos del proyecto de fin de máster, lo primero que debemos hacer (a parte de instalar toda la plataforma de desarrollo, incluido JDERobot) es comenzar a buscar un método suficientemente robusto para estimar el movimiento del robot usando únicamente un sensor óptico (sentido de la visión).

Debido a la calidad de las cámaras de vídeo (sobre todo en ambientes mal iluminados) deberán aplicarse filtros o usar algoritmos que presenten una buena robustez al ruido y que se adapten lo mejor posible al escenario propuesto (suelos lisos de la planta de un edificio).

Cuatro pionners en el circuito de cheste

Como experimento fin-de-práctica y para comprobar la seguridad dinámica del algoritmo de navegación he probado a meter cuatro robots pionner en el circuito de cheste para ver qué pasaba.

Para empezar todo iba bien exceptuando que algunas veces si ambos robots decidían sortear el obstáculo por el mismo lugar, al ponerse lado con lado, cuando recuperaban el rumbo chocaban debido a que a ciegas (dándose la espalda parcialmente) se habían colocado uno junto al otro.

Para solucionarlo he aumentado ligeramente en 20 mm el margen crítico y en 50 mm el margen de seguridad. De ese modo los robots no llegan a tocarse, pero tienen dificultad para pasar por el pasillo superior izquierdo debido a que es casi tan ancho como el margen de seguridad.

Me gustaría implementar un estimador de movimiento para detectar objetos en movimiento frente al robot y evitarlos con más antelación que un objeto estático. He pensado en hacer un estimador lineal como el que uso para corregir la dirección del siguelíneas o uno diferencial comparando la diferencia con los ángulos vecinos. Si termino por implementarlo expondré los resultados en el blog.

Detalles de interés en la práctica de navegación VFF

La práctica la entregué el lunes pasado, pero hasta hoy no me había dado cuenta que no tengo nada en el blog acerca de los detalles de la lógica de decisión que actúa sobre el algoritmo de navegación de nuestro Fernando Robonso y su fórmula R.

Toda la lógica de navegación gira en torno a dos cálculos:

• Campo de fuerzas virtuales (VFF - virtual force field): todo objeto alrededor del robot ejercerá una fuerza contra él que lo repelerá, evitando el obstáculo.
• Pasillo de seguridad: el robot sólo avanzará si frente a él hay un pasillo lo suficientemente ancho para pasar.

La unión de ambos cálculos conformará la lógica de decisión que decidirá en qué dirección debe girar el robot basándose en las fuerzas repulsivas que recibe y a qué velocidad avanza teniendo en cuenta la longitud del pasillo que tiene frente a él.

La lógica de decisión está implementada en una máquina de estados finita que está compuesta de tres estados:

• Estado "normal": Es aquél en el que el robot gira dependiendo de hacia dónde apunta el vector que forman las fuerzas de repulsión y la fuerza de atracción que siente del siguiente punto de control.
• Estado "rechazo": Es el estado en el que entra el robot al encontrarse con fuerzas frontales que le impiden avanzar normalmente hacia el objetivo. El robot procurará "rodear" el obstáculo dejando las fuerzas de repulsión a un lado en vez de detrás ignorando completamente el vector de atracción del punto de control.
• Estado de "estrechez": Es un estado especial en el que el robot reduce al mínimo su umbral del campo de fuerzas virtual de repulsión para que no oscile dentro de pasillos estrechos ni salte la repulsión dentro de él.

Quizá lo más complicado es ajustar los valores de los parámetros internos para "afinar" la navegación y ajustar los umbrales a los que el robot pasa de un estado a otro.

Durante todas las pruebas que he estado realizando he probado múltiples combinaciones (no todas de ellas se reflejan en el código final) y al final he implementado algunas mejoras secundarias para mejorar la navegación del robot.

Defensa de la calidad de la práctica:

• No se chocará nunca con un objeto frente al robot: Aunque el robot se dirija a gran velocidad hacia una esquina pequeña, cualquier objeto dentro del pasillo de seguridad hará que el robot reduzca la velocidad, evitando choques accidentales.
• No se chocará con un objeto lateral: debido al umbral crítico no se permitirá permanecer ningún objeto dentro del área que necesita el robot para maniobrar de modo que si el obstáculo no se mueve el robot no chocará contra él cuando gire en su sentido. En caso de que un objeto penetre el margen de crítico el robot dejará de moverse y entrará en estado de rechazo, evitando acercarse más al objeto debido a que el robot no se moverá hasta que pierda de vista el obstáculo que ha violado el espacio crítico.
• No chocará contra el fondo de un pasillo sin salida: debido al margen crítico y de seguridad, el robot no avanzará hacia el fondo de un pasillo sin salida e intentará salir de él a través del estado de repulsión a no ser que el camino de salida sea largo.
• Pasillos estrechos: el estado "estrechez" permite al robot pasar entre dos objetos que le dejen poco espacio para maniobrar, sin embargo como efecto secundario de los márgenes de seguridad y críticos el tamaño del pasillo mínimo es más elevado que en otras implementaciones precisamente por seguridad en la maniobra. Es decir, como el robot necesita un margen lateral más elevado para permitir que el "culo" no choque contra objetos mientras gira ésto limita el ancho del pasillo que considera el robot seguro para pasar.

Carreras por el pasillo del departamental

En esta versión he mejorado la estabilidad en velocidad comparando algunas opciones para determinar la velocidad a la que puede navegar el robot pioneer. Además, he usado un comparador con la velocidad anterior para suavizar los cambios bruscos.

Con esto he evitado el efecto "tembleque" que se produce cuando se modifica la velocidad del robot considerablemente en cada iteración.

Falta por mejorar el algoritmo VFF a uno que tenga en cuenta mejor la distancia a los objetos usando una ecuación trigonométrica y aunque la mejora en la decisión de giro hace que éste tome mejor las curvas sigue siendo lento debido al poco ángulo de visión y a que a poca distancia del objeto éste es plano en su parte inferior por el recorte de la cámara. Probaré a bajar la cámara un poco para evitar ese efecto a corta distancia.

Un problema que me encontraré si hago eso es que la regla de tres dejará de funcionar para estimar el ángulo al que se encuentra cada columna de la imagen y deberé hacer el cálculo por cada pixel. Para mejorar el rendimiento sólo calcularé el ángulo del último pixel de suelo en cada columna, pero aún así las cuentas se complican.

Navegación visual por el pasillo del departamental

Primer acercamiento a la navegación visual sin asistencia de líneas pintadas en el suelo.

Para llegar a una solución he pensado en implementar un algoritmo VFF basado en la distancia en la que se encuentran los objetos que aparecen en la imagen de la cámara de vídeo.

He estimado que la apertura de visión de la cámara es algo inferior a 70º, de modo que se puede estimar el ángulo al que se encuentra cada columna de la imagen con una simple regla de tres.

Queda por mejorar los "saltitos" o efecto "tembleque" que tiene el robot cuando ajusta su velocidad basada en el módulo del vector de repulsión y mejorar la decisión de giro, la encuentro demasiado lenta debido al poco ángulo de visión del que disponemos.

Sigue líneas visual con umbrales lineales

Por fin he puesto en marcha el introrob para gazebo. Tras tener problemas compilando el newintrorob2.tar.gz por fin descubro que simplemente hay que usar el mismo introrob que viene con jderobot 4.3.

En esta primera implementación creamos tres umbrales lineales que determinarán cómo se comportará el robot ante la tarea de seguir la línea roja.

En el siguiente vídeo muestro cómo se comporta el robot en el pequeño circuito incluido en las prácticas. Podría aumentar la velocidad un poco más, pero el robot pionner se vuelve muy inestable en los giros cerrados ya que tiende a volcar cuando gira, o a desviarse cuando frena o acelera bruscamente.

En la implementación inicial he incluido un algoritmo de compensación de inercia. Con él consigo dejar de girar antes de llegar al punto de destino, de modo que no me lo pase por la inercia de giro del robot. La estimación es lineal y usa únicamente el estado anterior para calcular la posición futura.

Comportamiento choca-gira: retoque final

Detecté pero no arreglé un pequeño problema derivado de calcular si ha llegado el robot o no al ángulo de destino. Ahora toca arreglar ese defecto para que la práctica sea completa.

Para comprender el problema debemos saber dos cosas del robot:

Los sensores de orientación del robot no son perfectos, por consiguiente la brújula tiene un margen de error y una granularidad que impide la búsqueda de un ángulo de destino perfecto. Por consiguiente no se busca un ángulo de destino, si no un ángulo de destino con un margen de error de varios grados.

En la imagen puede verse una representación del ángulo de destino:

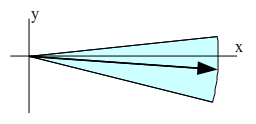
En ella puede verse el ángulo de destino (356º) y el margen de error anterior (356º - 10º = 346º) y posterior (356º + 10º = 366º = 6º).

¿Qué problema existe en la búsqueda de ese sentido de orientación?

Para averiguar si ha llegado o no el robot a su orientación de destino restamos los ángulos destino y actual y obtenemos el valor absoluto.

φ = | φ_r - φ_f |

Donde φ_r es la orientación actual del robot y φ_d la orientación final a la que debe llegar.

Veamos varios ejemplos de cómo se comporta este mecanismo de cálculo con varios ejemplos:

• Estamos en 340º: |340 - 356| = 16 (> 10 fuera del margen - CORRECTO).
• Estamos en 349º: |349 - 356| = 7 (< 10 dentro del marge - CORRECTO).
• Estamos en 358º: |340 - 356| = 2 (< 10 dentro del margen - CORRECTO).
• Estamos en 4º: |4 - 356| = 352 (> 10 fuera del margen - INCORRECTO).
• Estamos en 8º: |8 - 356| = 348 (> 10 fuera del margen - CORRECTO).

Podemos resumir el comportamiento de este cálculo en la siguiente ilustración:

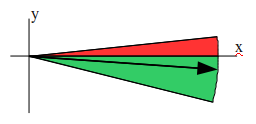
En ella podemos ver que cuando el ángulo es cercano al destino pero éste no "cruza" el eje de abscisas todo funciona correctamente (zona verde) pero si estamos dentro de un ángulo al otro lado del eje de abscisas entonces nos encontramos con que los cálculos fallan.

¿Cómo arreglarlo?

Existen varias soluciones. La que proponen en clase es comprobar cuándo el robot puede verse involucrado en este tipo de situaciones y modificar el cálculo de la diferencia en ese caso.

¿Cómo?

Veamos la siguiente ilustración:

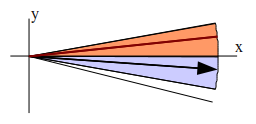
Podemos ver dos zonas la anaranjada y la azulada. Corresponden al arco comprendido entre 10º y 0º (zona anaranjada) y de 0º a -10º (zona azulada).

Podríamos hacer sectores y comprobar cuándo pasan por el eje de abscisas y arreglarlo. Una serie de sentencias condicionales nos ayudarían en la tarea.

Pero hay una forma más sencilla, comprobando únicamente cuándo el cálculo podría darnos problemas.

¿Cómo podríamos averiguar eso?

Podríamos hacer las siguientes comprobaciones:

• Si el robot está orientado en un ángulo inferior a 10º (zona anaranjada) y el destino es superior a 350º (zona azulada) le quitamos 360 grados al ángulo de destino.
• Si el robot está orientado en un ángulo superior a 350º (zona azulada) y el destino es inferior a 10º (zona anaranjada) le quitamos 360 grados al ángulo del robot.

Con eso los cálculos saldrían correctos. Podemos comprobarlo con los ejemplos anteriores.

Pensemos que la condición "el destino es superior a 350º" siempre se está cumpliendo de modo que sólo hay que restarle 360º al destino cuando el robot tiene su ángulo de giro por debajo de los 10º de margen:

• Estamos en 340º: |340 - 356| = 16 (> 10 fuera del margen - CORRECTO).
• Estamos en 349º: |349 - 356| = 7 (< 10 dentro del marge - CORRECTO).
• Estamos en 358º: |340 - 356| = 2 (< 10 dentro del margen - CORRECTO).
• Estamos en 4º: |4 - (356 - 360)| = |4 + 4)| = 8 (< 10 dentro del margen - CORRECTO).
• Estamos en 8º: |8 - (356 - 360)| = |8 + 4| = 12 (> 10 fuera del margen - CORRECTO).

¿Y no existe una solución más simple?

Casi siempre hay una solución mejor a la que inicialmente pensamos de forma natural.

Basta con restarle a 360º el ángulo calculado si éste supera los 180º.

Lo comprobamos con el ejemplo anterior:

• Estamos en 340º: |340 - 356| = 16 (> 10 fuera del margen - CORRECTO).
• Estamos en 349º: |349 - 356| = 7 (< 10 dentro del marge - CORRECTO).
• Estamos en 358º: |340 - 356| = 2 (< 10 dentro del margen - CORRECTO).
• Estamos en 4º: |4 - 356| = 352 -> 360 - 352 = 8 (< 10 dentro del margen - CORRECTO).
• Estamos en 8º: |8 - 356| = 348(*) -> 360 - 348 = 12 (> 10 fuera del margen - CORRECTO).

(*)Para minimizar el hitrate de dicha comprobación y ahorrarnos restas innecesarias comprobamos que únicamente esté por encima del margen superior, 350º, que será cuando nos interfiera en el cálculo en vez de hacerlo cada vez que supere los 180º.

En estos ejemplos hemos usado un error de 10º y hemos usado grados para facilitar los cálculos pero en la práctica el margen de error con el ángulo de destino es de tan sólo 5º y todos los cálculos se hacen en radianes.

En el siguiente vídeo muestro el funcionamiento del cálculo. Estamos calculando el ángulo de diferencia de manera continua, pero cuando la diferencia es mayor de 330º (360º - 30º) habilitamos el cálculo de corrección.

Hay que notar que en la práctica existen dos umbrales de decisión: <30º para girar más despacio y <5º para decidir que se ha llegado al objetivo. De modo que hay que tener en cuenta el umbral más bajo (360º - 30º) o no aplicar la optimización. De no hacerlo el robot podría pasar girando sobre los 5º de margen y pasarse en el giro, teniendo que completar una nueva vuelta y rezar que no vuelva a ocurrir lo mismo.

Entrenamientos en el circuito de Cheste

Hoy sólo he hecho una jornada de entrenamiento en el circuito de Cheste para comprobar si mi algoritmo de navegación local VFF es suficiente para recorrer el circuito..

Para recorrer el circuito aumenté un poco el margen desde el cual los obstáculos ejercen fuerzas de repulsión (arco verde) y aumenté la velocidad máxima cuando el destino está entre -30º y 30º. En la penúltima curva se ve claramente que la lógica de decisión necesita unos retoques para evitar comportamientos erráticos, aunque sean breves.

Dejaremos a Fernando Robonso y su fórmula R descansar un poco antes de pensar cómo mejorar la lógica de navegación.

Navegación local usando VFF (vectores de fuerzas de repulsión)

El algoritmo de vectores de fuerzas de repulsión basa su funcionamiento en fuerzas vectoriales que se oponen al movimiento frontal del robot creados por los obstáculos a su alrededor.

Cuando el robot no tiene ningún obstáculo frente a él la única fuerza que actúa sobre él es la atracción ejercida por el punto de destino (vector dirección).

Sin embargo conforme aparecen obstáculos, éstos ejercen una fuerza con dirección al robot y fuerza inversamente proporcional a su distancia. Eso provoca que los objetos lejanos empiecen a modificar la trayectoria del robot intentando que evite acercarse a ellos, pero conforme el robot se acerca a un obstáculo por estar en medio del camino éste ejerce cada vez más fuerza de repulsión hasta que ésta supera a la fuerza de atracción del destino, provocando que el robot se detenga y busque otro camino.

En la mayoría de los casos, si el objeto se encuentra en la tangente del trayecto, las fuerzas de repulsión modificarán la trayectoria del robot levemente sin hacer que éste se detenga para evitar la colisión.

En el siguiente vídeo se observa una implementación de la navegación local usando fuerzas VFF en el que la lógica de decisión realizará las siguientes acciones dependiendo del ángulo que tenga el vector resultante (la suma del vector de repulsión más el vector de navegación al destino). Hay que tener en cuenta que mientras un obstáculo no se encuentre dentro de la zona delimitada por el arco verde éste no ejercerá fuerzas de repulsión:

• Si el vector forma menos 30º respecto a la orientación del robot: El robot avanza a máxima velocidad corrigiendo levemente su trayectoria.
• Si el vector forma un ángulo comprendido entre 30º y 60º respecto al avance del robot: El robot modera su velocidad corrigiendo su trayectoria poco a poco.
• Si el ángulo que forma con el sentido de avance del robot es superior a 60º: el robot se detiene y gira con más velocidad para corregir el error de dirección.

Para evitar que el robot se comporte de manera errática cuando los vectores de dirección y repulsión se contrarrestan he agregado dos constantes. Una de ellas empuja constantemente al robot hacia delante sumándose al vector resultante anterior. Por otro lado si el módulo del vector resultante no supera una magnitud mínima entonces el robot avanza y gira como si el vector resultante y la trayectoria del robot formasen entre 30 y 60º (avanza con velocidad moderada mientras corrige la dirección).

En el siguiente vídeo puede observarse que la mejora funciona bien sin tener que complicar la lógica de decisión:

Comportamiento choca-gira con decisión de giro mejorada

En la segunda mejora he achatado los umbrales de seguridad (arco rojo) y de velocidad (umbral verde) pero, como modificación más importante, el algoritmo de decisión del sentido de giro ya no es completamente aleatorio.

Para decidir hacia qué sentido girar calculo la suma de distancias a obstáculos a derecha e izquierda del robot haciendo que éste gire hacia el sentido en el que la distancia media sea mayor. De este modo evitamos movimientos inútiles hacia esquinas de la habitación, permitiendo, a su vez, que decida ir en sentido de un pasillo en vez de ir contra las paredes de forma aleatoria.

El arco que recorremos para dicha decisión es el comprendido entre los grados 30 y 90 a ambos lados del robot. El ángulo de giro aleatorio también estará comprendido entre esos ángulos.

El el vídeo podemos observar que ahora el robot ha recorrido una mayor superficie de nuestro mundo virtual gracias a evitar giros muy cortos que apenas mejoran la posición respecto del obstáculo o aquellos que lo llevan frente a un obstáculo, pared o esquina.

Comportamiento choca-gira con velocidad variable

La primera mejora que he implementado es un control de velocidad basado en el entorno que reduce la velocidad en caso de existir un objeto dentro de la zona de seguridad.

Las zonas de seguridad (arco verde) y de evasión de colisión (arco rojo) tienen el centro adelantado para permitir pasar al robot por zonas estrechas a la vez que minimizan la posibilidad de colisión frontal.

La próxima mejora será una búsqueda algo más "inteligente" del sentido de giro. Seguirá siendo aleatorio pero dotaremos de cierta inteligencia al sentido de giro y limitaremos el ángulo para evitar giros casi nulos o giros demasiado amplios.

Comportamiento choca-gira básico

En este primer intento he implementado una versión muy básica del comportamiento "choca-gira" en el que el robot se mueve por el mundo usando una máquina de estados finitos que tiene los siguientes tres estados:

1. Estado "avanza": El robot avanza por el mundo en línea recta a velocidad constante. En el momento que se detecta un objeto más cercano de un umbral se pasa al estado "retrocede" para evitar la colisión.
2. Estado "retrocede": El robot retrocede durante un número definido de iteraciones antes de pasar al estado "gira".
3. Estado "gira": El robot gira un ángulo aleatorio para tratar de sortear el obstáculo. Una vez girado el ángulo deseado el robot volverá al estado "avanza".

La siguiente ilustración muestra gráficamente la relación entre los estados:

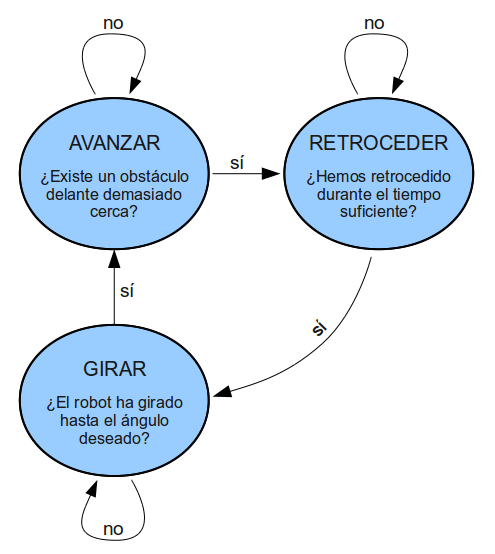
En el siguiente vídeo puede observarse el comportamiento del robot usando este algoritmo en su versión más básica:

En la siguiente versión trataré de optimizar el algoritmo con algunas mejoras como: velocidad variable dependiendo del entorno y giro hacia el lado con más espacio.

Instalación completada

A día de hoy he completado la instalación del entorno de desarrollo y simulación: player 2.0.5 + stage 2.0.4 + gazebo 0.7.0 + jderobot 4.3.0 y realizada la primera compilación del schema introrob.

A continuación preparo las imágenes y explicaciones del primer ejercicio y las múltiples variantes (o mejoras) implementadas: el comportamiento choca-gira.